Prefix Sum Technique Notes
Idea
- Start from 0
- Start from 1
Prefix sum is to create an array prefix where prefix[i] is the sum of all elements up to the index i (inclusive).
nums = [5, 2, 1, 6, 3, 8];
pref = [5, 7, 8, 14, 17, 25];
# delay
pref = [0, 5, 7, 8, 14, 17, 25];
Sometimes, we use a delay-prefix array which start from index 1. This is convenient when calculating distance or length.
Prefix sums allow us to find the sum of any subarray in $O(1)$. If we want the sum of the subarray from i to j (inclusive), the answer is prefix[j] - prefix[i-1], or prefix[j] - prefix[i] + nums[i].
Behind the idea
Building a prefix sum is a form of pre-processing.
Pre-processing is a useful strategy in a variety of problems where we store pre-computed data in a data structure before running the main logic of our algorithm.
What’s other pre-processing strategies?
Problems
Number of Ways to Split Array
Ask: left inclusive sum larger than or equal to right exclusive sum. (0 <= i < N -1)
You are given a 0-indexed integer array nums of length n.
nums contains a valid split at index i if the following are true:
- The sum of the first
i + 1elements is greater than or equal to the sum of the lastn - i - 1elements. - There is at least one element to the right of
i. That is,0 <= i < n - 1.
Return the number of valid splits in nums.
Example 1:
Input: nums = [10,4,-8,7]
Output: 2
Explanation:
There are three ways of splitting nums into two non-empty parts:
- Split nums at index 0. Then, the first part is [10], and its sum is 10. The second part is [4,-8,7], and its sum is 3. Since 10 >= 3, i = 0 is a valid split.
- Split nums at index 1. Then, the first part is [10,4], and its sum is 14. The second part is [-8,7], and its sum is -1. Since 14 >= -1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is [10,4,-8], and its sum is 6. The second part is [7], and its sum is 7. Since 6 < 7, i = 2 is not a valid split. Thus, the number of valid splits in nums is 2.
Method:
The requirement can be stated as prefix[i] >= prefix[N-1] - prefix[i].
Since no need to record length, we use 0-start prefix.
class Solution {
public int waysToSplitArray(int[] nums) {
// build the prefix sum
int N = nums.length;
long[] prefix = new long[N];
prefix[0] = nums[0];
for (int i = 1; i < N; i++) {
prefix[i] = nums[i] + prefix[i-1];
}
// Extract subarray sum:
// i:j (inclusive) = prefix[j] - prefix[i-1] = prefix[j] - prefix[i] + nums[i]
int ways = 0;
for (int i = 0; i < N - 1; i++) {
if (prefix[i] >= prefix[N-1] - prefix[i]) {
ways++;
}
}
return ways;
}
}
Contiguous Array
- maximum length of subarray
- subarray valid by equal number of
0and1(input array is binary array)
Given a binary array nums, return the maximum length of a contiguous subarray with an equal number of 0 and 1.
Example 2:
Input: nums = [0,1,0]
Output: 2
Explanation: [0, 1] (or [1, 0]) is a longest contiguous subarray with equal number of 0 and 1.
Method:
- To calculate length, we need index. It’s very intuitive to think of 2 pointers and sliding window, but that’s not for this problem.
- 2 pointer needs the input be sorted, not for this problem
- sliding window: the valid criteria is hard to maintain when expanding the window (no way to decide to move any bound)
- Directly using prefix sum is impossible as 0 in array do not contribute to sum
- Replace 0 with -1
- Use a variable tracking prefix sum, and increment the variable conditionally (ternary operator, -1, 1)
- Need a hashmap to store the index. Only need leftmost index as we want longest subarray
- Iterate along the array, if we meet a prefix sum existing before, means there’s a subarray with sum = 0 (valid condition), then we update the
maxLen - Met this prefix sum first time, put it into map with index
- Iterate along the array, if we meet a prefix sum existing before, means there’s a subarray with sum = 0 (valid condition), then we update the
/**
use count variable to record prefix sum
use fill -1 array to test runtime with count
filled -1 array is a little quicker than count wich ternary operator
*/
class Solution {
public int findMaxLength(int[] nums) {
for (int i = 0; i < nums.length; i++) {
if (nums[i] == 0) nums[i] = -1;
}
Map<Integer, Integer> map = new HashMap<>();
map.put(0, -1); // Used to track subarray start from first element
int maxLen = 0, pre = 0;
for (int i = 0; i < nums.length; i++) {
// if use count: count += nums[i] == 0? -1 : 1;
pre += nums[i];
if (map.containsKey(pre)) {
maxLen = Math.max(maxLen, i - map.get(pre));
} else {
map.put(pre, i);
}
}
return maxLen;
}
Product of Array Except Self
- return the product of all elements except
nums[i] - $O(n)$ time algorithm without using division operation
Given an integer array nums, return an array answer such that answer[i] is equal to the product of all the elements of nums except nums[i].
The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer.
You must write an algorithm that runs in O(n) time and without using the division operation.
Example 1:
Input: nums = [1,2,3,4]
Output: [24,12,8,6]
Method:
- subarray product instead of sum
- A very important transition: the product except current element is equal to left product and right product exclusively
- We can use two extra array, one is prefix product from left, the other is prefix product from right, then multiply two accordingly
- Follow-up: we can move from left to right then backwards, get same output
/**
* two extra array
*/
class Solution {
public int[] productExceptSelf(int[] nums) {
int N = nums.length;
int[] leftP = new int[N+1];
int[] rightP = new int[N+1];
leftP[0] = 1;
rightP[N] = 1;
for (int i = 0; i < N; i++) {
leftP[i+1] = leftP[i] * nums[i];
}
for (int i = N - 1; i >= 0; i--) {
rightP[i] = rightP[i+1] * nums[i];
}
int[] res = new int[N];
for (int i = 0; i < N; i++) {
res[i] = leftP[i] * rightP[i+1];
}
return res;
}
}
/**
* forwards then backwards
*/
class Solution {
public int[] productExceptSelf(int[] nums) {
int N = nums.length;
int[] res = new int[N];
res[0] = 1;
for (int i = 1; i < N; i++) {
res[i] = res[i-1] * nums[i-1];
}
int suffix = 1;
for (int i = N - 1; i >= 0; i--) {
res[i] *= suffix;
suffix *= nums[i];
}
return res;
}
}
Binary Subarrays With Sum
- subarray with exact criteria —
sum == goal - ask number of subarrays
Given a binary array nums and an integer goal, return the number of non-empty subarrays with a sum goal.
A subarray is a contiguous part of the array.
Example 1:
Input: nums = [1,0,1,0,1], goal = 2
Output: 4
Explanation: The 4 subarrays are bolded and underlined below:
[1,0,1,0,1]
[1,0,1,0,1]
[1,0,1,0,1]
[1,0,1,0,1]
Method:
- sliding window
- Intuition: number of subarray, we think of a trick in sliding window that given
(left, right)window, there’reright - left + 1subarrays end withright. But inside the bound, the sum of subarray is less than or equal to the goal - If we could get number of subarrays that have sum less than goal, how can we solve this problem?
- If we additionally compute number of subarrays that have sum less than
goal - 1, then subtract two value, we could get number of exactly equal togoal
- prefix sum
- sum of subarray can be derived by prefix sum
- Ask the number of subarray, can be put into count of valid prefix-sum, like two sum with hashmap
- use hashmap, key is prefix sum, value is count
- when met target value
(prefix[i] - prefix[i-1] == goal), the answer increment by the count
// method 1: sliding window
// if goal == 0, one pass
// if goal > 0, check goal - (goal-1)
class Solution {
int[] nums;
public int numSubarraysWithSum(int[] nums, int goal) {
this.nums = nums;
if (goal == 0) return atMostGoal(0);
return atMostGoal(goal) - atMostGoal(goal - 1);
}
private int atMostGoal(int k) {
int left = 0;
int ans = 0;
int curSum = 0;
for (int right = 0; right < nums.length; right++) {
curSum += nums[right];
while (curSum > k) {
curSum -= nums[left];
left++;
}
ans += right - left + 1;
}
return ans;
}
}
// method 2: prefix sum
class Solution {
public int numSubarraysWithSum(int[] nums, int goal) {
Map<Integer, Integer> map = new HashMap<>();
// Use map<prefix-sum, count> to calculate numbers of subarray
int res = 0;
map.put(0, 1); //before prefix sum, start with 0 and count-1;
int pre = 0;
for (int i = 0; i < nums.length; i++) {
pre += nums[i];
// prefix[j] - prefix[i-1] == goal -> (i,j) -> valid
if (map.containsKey(pre - goal)) {
res += map.get(pre - goal);
}
map.put(pre, map.getOrDefault(pre, 0) + 1);
}
return res;
}
follow up: This problem is almost the same :Subarray Sum Equals K .
(Hard) Number of Submatrices That Sum to Target
From 1-D to 2-D, now we come the sub-matrices sum.
Given a matrix and a target, return the number of non-empty submatrices that sum to target.
A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.
Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.
Example 1:
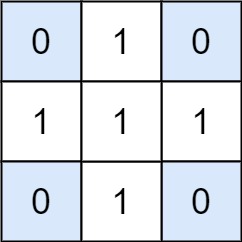
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.
Method:
If we know how to calculate 1-D array subarray sum numbers, how to apply it in 2-D array?
- We still need map to record the previous sum appearance and its count (frequency)
- We can modify the matrix directly as well as create a new one, to calculate its row-prefix-sum
- Compute 1-D array from each row, 2-D array start from each row, apparently 3-levels loop
- Quite like 1-D array, the originally index now becomes column-index
- The most difficult part is to think 2-D in 1-D array, arrange the loop (row, column)
class Solution {
public int numSubmatrixSumTarget(int[][] matrix, int target) {
int m = matrix.length;
int n = matrix[0].length;
for (int i = 0; i < m; i++) {
for (int j = 1; j < n; j++) {
matrix[i][j] += matrix[i][j-1];
}
}
// now have row-specfic prefix sum
Map<Integer, Integer> map = new HashMap<>();
int res = 0;
// Caution! Reflex on 1-D array, two pointer
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
map.clear();
map.put(0, 1);
int pre = 0;
for (int k = 0; k < m; k++) {
pre += matrix[k][j] - (i == 0 ? 0 : matrix[k][i-1]);
res += map.getOrDefault(pre - target , 0);
map.put(pre, map.getOrDefault(pre, 0) +1);
}
}
}
return res;
}
}